13.4.1. Introduction ↩

Parzen classifier estimates probability density for each class using a non-parametric approach based on stored training examples. When computing output for a new observation, the contribution of each training example is integrated. The contribution is modeled by a kernel function and is influenced by the smoothing parameter (kernel width).

By default, sdparzen trains a Parzen classifier with Laplace kernel function which is less computationally demanding than frequently-adopted Gaussian kernel. Smoothing parameter is optimized using EM algorithm optimizing cross-validated log-likelihood.

>> load fruit
260 by 2 sddata, 3 classes: 'apple'(100) 'banana'(100) 'stone'(60) 

>> p=sdparzen(a)
.....sequential pipeline       2x1 'Parzen model+Decision'
1 Parzen model            2x3  260 prototypes, h=0.8
2 Decision                3x1  weighting, 3 classes

>> sdscatter(a,p)

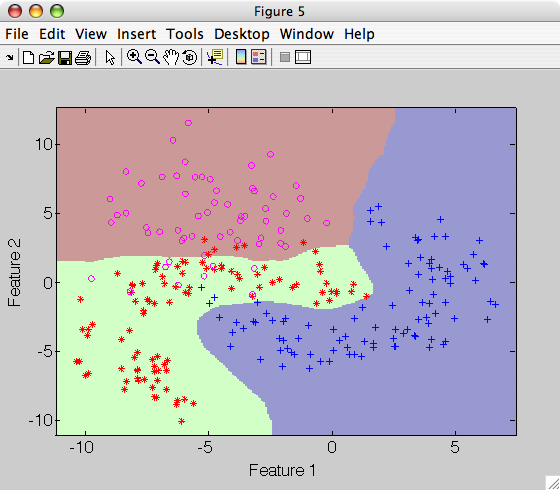
The default Parzen classifier uses scalar smoothing i.e. equal kernel width for each feature. Smoothing parameter is accessible in h field of Parzen pipeline:

>> p(1)'
Parzen model pipeline   2x3
 1 Parzen model            2x3  260 prototypes, h=0.8
       inlab: '1','2'
         lab: 'apple','banana','stone'
      output: probability density
           h: smoothing parameter

13.4.2. Adjusting smoothing parameter manually ↩

Smoothing may be fixed manually. This is advantageous for quick experimentation because it skips the time-consuming EM algorithm.

Here we use very small kernel with:

>> p=sdparzen(a,'h',0.04)

>> sdscatter(a,p)

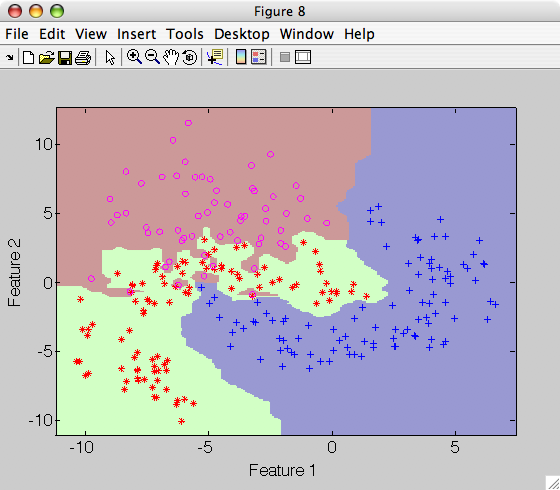
Note that the decision boundary becomes very complicated emphasizing very local changes of the class distributions.

13.4.3. Vector smoothing ↩

Smoothing parameter may be also estimated for each dimension, specifying h as vector:

>> p=sdparzen(a,'h','vector')
.............sequential pipeline       2x1 'Parzen model+Decision'
 1 Parzen model            2x3  260 prototypes, vector smoothing
 2 Decision                3x1  weighting, 3 classes

>> p(1).h

ans =

    0.6265    1.0200

Vector smoothing requires extra multiplication for each dimension of each training sample. Alternative strategy is to scale the data to unit variance with sdscale so that scalar smoothing is sufficient.